

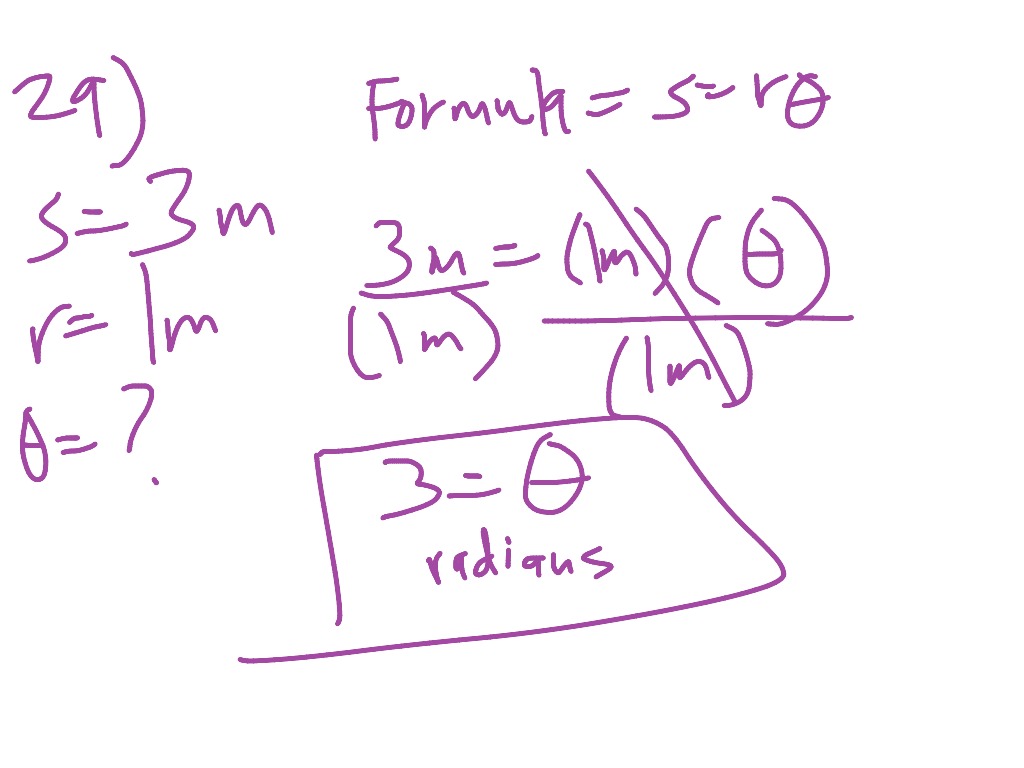
That we can approximately with things like lines and This, what we could do is we can break it up into Integration, integral calculus is teaching us is that when we see something that's changing like So how can we do it? Well, the one thing that Is okay, that's going to be from x equals a to xĮquals b along this curve. If we lay a string along the curve, what would be theĭistance right over here? That's what I'm talkingĪbout by arc length. Line but instead we want to find the distance along the curve.
#Arc length calculator calculus how to#
Know already how to find the distance in the straight This point right over here, not a straight line, we On the graph of a function, and if I were to go at What do I mean by that? Well, if I start at this point What I want to do now is to see if we can use the definitive role

We've used the definite integral to find areas. If that is true, it seems that, as long as you want to measure some property of the curve, if you can express it in dx, you're good to go. It seems to me the only way that the Fundamental theorem of calculus holds. The area of that function represent the arc length. Put in other words, the new function that is created is actually a function where we evaluate the area from. Or can it vary? Should we read the Riemann sum as a sum of f(x)dx, or can we read it as the sum of f(x), multiplied by dx?ģ) Even though people in the comments say this is not about area anymore, I like to still see it that way: Sal seems to transform this function from something that is expressed in terms of arc length into a different function that is expressed as area. It is in fact lim dx->0 dx.Ģ) dx represents a fixed quantity, as in: the width of the rectangles are constant for the integral. It represents the infinitely small width of the rectangle. Can someone confirm the following things?ġ) In the integral notation ∫ f(x) dx, dx is not just a notation, but an actual quantity that gets multiplied while summing the Riemann Sum. Together with the Q/A in this forum I think I've been able to tie the pieces together a bit. Using official modern definitions, one nautical mile is exactly 1.I think Sal is making a huge jump here, skipping over things we should have learned. For example, they imply that one kilometre is exactly 0.54 nautical miles. Those definitions of the metre and the nautical mile have been superseded by more precise ones, but the original definitions are still accurate enough for conceptual purposes and some calculations.
Those are the numbers of the corresponding angle units in one complete turn. The lengths of the distance units were chosen to make the circumference of the Earth equal 40 000 kilometres, or 21 600 nautical miles. If a curve can be parameterized as an injective and continuously differentiable function (i.e., the derivative is a continuous function) f : → R n is in gradians. A rectifiable curve has a finite number of segments in its rectification (so the curve has a finite length). Arc length s of a logarithmic spiral as a function of its parameter θ.Īrc length is the distance between two points along a section of a curve.ĭetermining the length of an irregular arc segment by approximating the arc segment as connected (straight) line segments is also called curve rectification. Distance along a curve When rectified, the curve gives a straight line segment with the same length as the curve's arc length.


 0 kommentar(er)
0 kommentar(er)
